PROGRAMACIÓN LINEAL

INTRODUCCIÓN A LA PROGRAMACIÓN LINEAL

         OBJETIVOS GENERALES :

       1. Que los usuarios que visiten nuestro blog les sirva como facilitador o guía en los siguientes                  problemas  que hemos planteado del tema programación lineal.

       2. Calcular los problemas de programación lineal planteando una variedad de técnicas que sea                 entendibles para nuestros usuarios

       3. Elaborar un concepto detallado  de programación lineal y sus propiedades generales.

          CONCEPTO :

• La programación lineal es el conjunto de técnicas matemáticas que pretenden optimizar (maximizar o minimizar) una función objetivo, sujeta a una serie de restricciones, expresadas por inecuaciones lineales, para obtener el mayor beneficio o menor coste.

• OPTIMIZAR: es determinar la mejor manera de realizar una actividad, con el uso eficiente de los recursos disponibles. Matemáticamente podemos decir que optimizar es maximizar o minimizar.

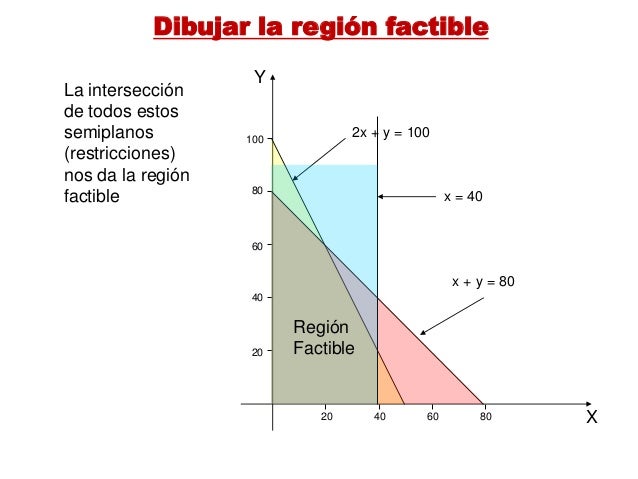
         RECOMENDACIONES PARA RESOLVER UNA APLICACIÓN DE                                                 PROGRAMACIÓN LINEAL :

       1 ) Escribir la función objetivo y todas las restricciones necesarias.

        2) Graficar la región de soluciones y determinar la región factible.

        3)  Identificar los vértices.

        4) Encontrar el valor de la función objetivo en cada vértice.

        5) Ofrecer la solución que está dada por el vértice que produce el valor óptimo de la función objetivo.

     
          BIBLIOGRAFÍA 

•           ( Hoffman, Bradley, Sobecki, Price, Sandoval., Matemática aplicada a la administración               y  los  negocios)   -   año2010
•            Material  de clase - semana 10 ( Introducción a la programación lineal)

EJERCICIO 4

EJERCICIO 3

EJERCICIO 2

LÍMITES

          CONCEPTO :

• En análisis real y complejo, el concepto de límite es la clave de toque que formaliza la noción intuitiva de aproximación hacia un punto concreto de una sucesión o una función, a medida que los parámetros de esa sucesión o función se acercan a un determinado valor.
• Para fórmulas, el limite se utiliza usualmente de forma abreviada mediante lim como en lim(a_n) = a o se separa mediante la flecha (→) como en a_n → a.

   

  Evaluación Algebraica de Límites: Límites cuando x → a

•          CASO I:

                Si la función dada, esta totalmente simplificada, se sustituye directamente el valor a que                      tiende la variable independiente en la función, dando lugar al  limite buscado. 

           

         Ejm:   Calcular 

          SOLUCIÓN:

      

•         CASO II:

                Formas indeterminadas del tipo (0/0)

            Ejm:   Calcular 

 = 0 / 0


           SOLUCIÓN:

         

•          CASO III:

  Para calcular el limite de una función dada, es necesario simplificar mediante la                                      racionalización del numerador o del denominador, antes de sustituir el valor de la                                 variable independiente, de no hacerlo se dará la forma (0/0).

                Ejm: Calcular 

                SOLUCIÓN:

         RACIONALIZAMOS:

                                   

  EJERCICIOS DE LÍMITES

• Calcular el límite en función de "x" .

PROBLEMAS DE LÍMITES

PROBLEMA N°1:

              

   

https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgjUWuzubMGC2st_wxjb6LmpRXNNVCaAvSwAFvhOG0FWUPxemVU96Xz-6nWAZ8ZqmwiQyMkRjHhfv2_bEhoZL7gEbHSIWpSx7pZboqVLwwKiM70YmiJ82bq-6WcVZwFkwUtN1Abc6oId5ki/s1600/16df2077-fc52-4e6b-998a-f85717e14239.jpg

PROBLEMA N°2:

https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhm8_c_FjYiSSkPMyQuu3s8TaUSXXowzX8UMIfyXzhzfYY2SL4cvt0D97nfJKV6hBuIioBiosnU69AiNL7tunXOnJBc70dV2zGIkqoGV4TIZjjpIFnDx7jv0jpEcQ8FV63mjqLe77U1UJmi/s1600/7.jpg

LINK DE APOYO:

•       Problemas con límites

              [en línea] https://es.scribd.com/doc/3594460/PROBLEMAS-CON-LIMITES? fbclid=IwAR0bG138nRhtPzu-ovC5rHYkkYFlB-B7pozLxYVn1oK27t3QNhfkcjHOrK8

LÍMITES LATERALES

         Forma de un límite lateral:

Para que exista el límite de una función, deben existir los límites laterales y coincidir.

El significado de los signos en la notación para límites laterales se interpreta de la siguiente manera

• x ® a^- significa que x tiende aA tomando valores menores que a, es decir valores que se encuentran a su izquierda.

• x ® a⁺ significa que x tiende a A tomando valores mayores que a, es decir valores que se encuentran a su derecha.

EJERCICIO DE LÍMITES LATERALES 

                                                             
                                                            HALLAR:

1.- Sea la función:

https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEghT5GS6RoQJCI8e7D_8tBI5yBlpsguFB8cTZoXtvoQElJy1J0JYXJvRZHo9Qaq7j4I9vHFiLKC40aJc-bZ8cB-fZErRzqwkByzR14EoJz0xdHril6o_WLN38NhSnIbLH6qmEoEksV53GDm/s1600/5.jpg

Link de apoyo:     https://www.edu.xunta.gal/centros/iesfontemalbei/aulavirtual2/mod/book/view.php?id=2420

PROBLEMAS DE LÍMITES LATERALES

PROBLEMA N°1:

https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjqlHngGJB1RolFNwy8mkl5A-ACA6KRQek76x3UMCo8tXB3QdVgPSczgIsb3L27NKTHT5dmYMiIpvXA0fyM_dxVVNSmv87WlRaPpBzz4_2TjTaQU2PSSB9Nd6MQsB9KzVSm-zT9j2NYCicP/s1600/RENZO.jpg

PROBLEMA N°2:

Para el año 2000 las empresas de electricidades EESA y EDELNOR plántea uniformarsus tarifas eléctricas proyectando la tarifa residencial de s/. 26 y un cargo de 25 céntimos por cada kW si no sobrepasa los 350kwh y u n cargo de 45 céntimos  por cada  kW. sobre los 350kwh.

A)   Construya la función costo del consumo eléctrico mensual en  función de los Kw.

B)   HALLAR Lim_x→500f_{(x)   y Limx→350}f_(x).

https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEggy4rXBAycO2znn8fGHMp2kzJ20ofdF8kuXvtqIlwjtmsf1cE5QVGgj92OF7xWTsDN2bpOyIZUY3OyQ8Liz_koW4KmOxQEpGzyYWLhaXLVSOVMDg2C8ecpMvZdkVk9uijC2CllkPbdtz1h/s1600/RENZO+2.jpg

BIBLIOGRAFÍA:  ( Hoffman, Bradley, Sobecki, Price, Sandoval., Matemática aplicada a la negocios, las ciencias sociales y de la vida